2.1 Kirchhoffova zakona v kompleksni obliki

Iz e-ELEKTROTEHNIKA plus

Da bi mogli pristopiti k analizi izmeničnih vezij strnjenih elementov s kazalci, potrebujemo tudi kompleksni obliki Kirchhoffovih zakonov. Ker pa v strnjenem vezju območje spojišča ni prostor, kjer bi se kopičil naboj, in tudi zanka ni rob ploskve, ki bi jo prečkalo magnetno polje, veljata za splošno spojišče ali splošno zanko enačbi, ki ju že poznamo:

in .

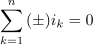
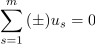
Izvajanje nadaljujmo s tokovno enačbo (v mislih pa imejmo tudi napetostno). Če so toki v vezju harmonični, je

.

Vsota kazalcev tokov je kazalec. Ker je množen s časovno funkcijo, je izraz v zunanjem oklepaju kazalec, ki se vrti, njegov realni del pa bo vsak trenutek enak nič le in samo, če bo ničelna njegova absolutna vrednost:

in .

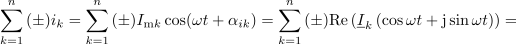
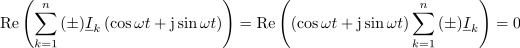
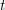
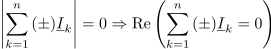
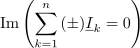
Absolutna vrednost kazalca je enaka nič le in samo, če to velja tudi za njegov realni in njegov imaginarni del oziroma za vsoto kazalcev kot celoto. Iz tega sledi sklep: za kazalce tokov v spojišču in za kazalce napetosti v zanki veljata enačbi

in ,

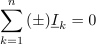
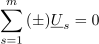
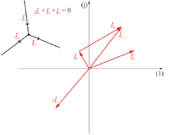
ki predstavljata Kirchhoffova zakona v kompleksni obliki (slika 22).

Podpoglavja:

• 2.1.1 Upor (kazalci)
• 2.1.2 Kondenzator (kazalci)
• 2.1.3 Tuljava (kazalci)

2 Lastnost in zakonitosti izmeničnih krogov (višji nivo)

2.1.1 Upor (kazalci)